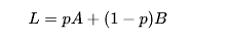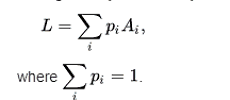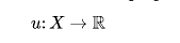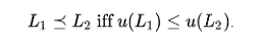теория полезности

определение понятие значение информация система структура принцип слово знак

НЕОКОНОМИКА

Ортодоксальные - марксизм и economics

• трудовая теория стоимости

• теория предельной полезности

• полезность
• утилитаризм

• полезность википедия теория полезности
• Utility утилитаризм в википедии

В economics (Замечание от ВТ: Вообще-то современную экономическую мысль на Западе называют термином - неоклассическая экономическая теория, а ЭКОНОМИКС осталось в англосаксонских странах, и Гугл не прав, когда переводит эту бессмысленную словоформу как "экономическая наука".) понятие полезности используется для моделирования стоимости или ценности. Его использование значительно эволюционировало с течением времени. Этот термин был первоначально введен как мера удовольствия или удовлетворения в рамках теории утилитаризма такими философами морали, как Иеремия Бентам и Джон Стюарт Милль. Этот термин был адаптирован и вновь применен в рамках неоклассической экономической теории, которая доминирует в современной экономической науке, как функция полезности это представляет собой заказ предпочтений потребителя по набору вариантов. Таким образом, полезность стала более абстрактным понятием, которое не обязательно основывается исключительно на получаемом счастье или удовольствии. (Вариант: Он лишен своей первоначальной интерпретации как измерение удовольствия или удовлетворения, полученного потребителем от этого выбора.)

Содержание

1 функция полезности

2 приложения

3 выявленные предпочтения

4 функции

4.1 кардинал

4.2 порядковый номер

4.3 предпочтения

4.4 выявленные предпочтения в области финансов

4.5 примеры

5 ожидаемая полезность

5.1 von Neumann–Morgenstern

5.2 Как вероятность успеха

6 косвенная полезность

6.1 деньги

7 Обсуждение и критика

8 см. также

9 ссылок

10 дальнейшее чтение

11 внешние ссылки

Рассмотрим набор альтернатив, с которыми сталкивается индивид и по которым индивид имеет порядок предпочтений. Функция полезности может представлять эти предпочтения, если существует возможность присвоить действительное число каждой альтернативе таким образом, что альтернативе a присваивается число, большее, чем альтернативе b, если и только если индивид предпочитает альтернативу a альтернативе b. В этой ситуации человек, который выбирает наиболее предпочтительную альтернативу, обязательно также выбирает альтернативу, которая максимизирует соответствующую функцию полезности. В общих экономических терминах функция полезности измеряет предпочтения в отношении набора товаров и услуг. Часто полезность соотносится с такими словами, как счастье, удовлетворение и благосостояние, и их трудно измерить математически. Таким образом, экономисты используют потребительские корзины предпочтений для измерения этих абстрактных, не поддающихся количественной оценке идей.

Жерар Дебре точно определил условия, необходимые для того, чтобы порядок предпочтений был представлен функцией полезности.[1] для конечного набора альтернатив они требуют только того, чтобы порядок предпочтений был полным (поэтому индивид может определить, какая из любых двух альтернатив предпочтительнее или что они одинаково предпочтительны), и что порядок предпочтений является транзитивным.

Полезность обычно применяется экономистами в таких конструкциях, как кривая безразличия, которая описывает комбинацию товаров, которую индивид или общество приняли бы для поддержания заданного уровня удовлетворения. Кривые полезности и безразличия используются экономистами для понимания оснований кривых спроса, которые являются половиной анализа спроса и предложения, используемого для анализа функционирования товарных рынков.

Индивидуальная полезность и социальная полезность могут быть истолкованы как значение функции полезности и функции социального обеспечения соответственно. В сочетании с производственными или товарными ограничениями, при некоторых предположениях эти функции могут быть использованы для анализа эффективности Парето, например, проиллюстрированы коробками Эджворта в кривых контрактов. Такая эффективность является центральным понятием в экономике благосостояния.

В финансах полезность применяется для формирования индивидуальной цены для актива, называемого ценой безразличия. Функции полезности также связаны с мерами риска, причем наиболее распространенным примером является энтропийная мера риска.

В области искусственного интеллекта функции полезности используются для передачи ценности различных результатов интеллектуальным агентам. Это позволяет агентам планировать действия с целью максимизации полезности (или "ценности") доступных вариантов выбора.

Было признано, что полезность не может быть измерена или наблюдаема непосредственно, поэтому вместо этого экономисты разработали способ вывести лежащие в основе относительные полезности из наблюдаемого выбора. Эти "выявленные предпочтения", как их назвал Пол Самуэльсон, проявлялись, например, в готовности людей платить:

Полезность принимается за корреляцию с желанием или желанием. Мы уже говорили о том, что желания нельзя измерить непосредственно, а только косвенно теми внешними явлениями, которые они порождают, и что в тех случаях, которые главным образом касаются экономики, мерилом служит цена, которую человек готов заплатить за исполнение или удовлетворение своего желания.[2]:78

Существует некоторое противоречие в вопросе о том, можно ли измерить полезность того или иного товара. Одно время считалось, что потребитель может точно сказать, сколько полезности он получил от товара. Экономисты, которые сделали это предположение, принадлежали к "кардиналистской школе" экономикс. Сегодня функции полезности, выражающие полезность в зависимости от количества различных потребляемых товаров, рассматриваются либо как кардинальные, либо как порядковые (ординальные), в зависимости от того, интерпретируются ли они как предоставляющие больше информации, чем просто ранговое упорядочение предпочтений по пачкам товаров, например, информацию о силе предпочтений.

Основная статья: Cardinal utility кардиналистская теория полезности

Когда используется кардинальная полезность, величина различий полезности рассматривается как этически или поведенчески значимая величина. Например, предположим, что чашка апельсинового сока имеет полезность 120 utils, чашка чая имеет полезность 80 utils, а чашка воды имеет полезность 40 utils. С кардинальной полезностью можно сделать вывод, что чашка апельсинового сока лучше чашки чая ровно на столько же, на сколько чашка чая лучше чашки воды. Формально говоря, это означает, что если у кого-то есть чашка чая, то он готов принять любую ставку, с вероятностью p большей, чем 5, чтобы получить чашку сока, с риском получить чашку воды, равным 1-p. Однако нельзя заключить, что чашка чая составляет две трети полезности чашки сока, потому что этот вывод будет зависеть не только от величины различий полезности, но и от "нуля" полезности. Например, если бы "ноль" полезности находился на отметке - 40, то чашка апельсинового сока была бы на 160 utils больше нуля, чашка чая на 120 utils больше нуля. Кардинальная полезность для экономики может рассматриваться как предположение, что полезность может быть измерена через количественные характеристики, такие как рост, вес, температура и т. д.

Неоклассическая теория в значительной степени отошла от использования кардинальных функций полезности в качестве основы экономического поведения. Заметным исключением является анализ выбора в условиях риска (см. ниже).

Иногда кардинальная полезность используется для агрегирования полезностей между людьми, для создания функции социального обеспечения.

Основная статья: Ordinal utility (Ординалистская теория полезности)

Когда используются порядковые утилиты, различия в utils (значениях, принятых функцией полезности) рассматриваются как этически или поведенчески бессмысленные: индекс полезности кодирует полный поведенческий порядок между членами набора выбора, но ничего не говорит о связанной силе предпочтений. В приведенном выше примере можно было бы только сказать, что сок предпочтительнее чая воде, но не более. Таким образом, порядковая полезность использует сравнения, такие как "предпочтительнее", "не больше", "меньше" и т. д.

Порядковые функции полезности уникальны вплоть до возрастающих монотонных (или монотонных) преобразований. Например, если функция u(x) берется как порядковая, она эквивалентна функции u(x)³, потому что взятие 3-й степени является возрастающим монотонным преобразованием (или монотонным преобразованием). Это означает, что порядковое предпочтение, индуцируемое этими функциями, одно и то же (хотя это две разные функции). В отличие от этого, кардинальные утилиты уникальны только до возрастающих линейных преобразований, поэтому если u(x) их принимать за кардинальные, то они не эквивалентны u(x)³.

Хотя предпочтения являются общепринятой основой микроэкономики, часто бывает удобно представлять предпочтения с помощью функции полезности и косвенно анализировать поведение человека с помощью функций полезности. Пусть X - это набор потребления, набор всех взаимоисключающих корзин, которые потребитель может себе представить. Функция полезности потребителя u:X -> R ранжирует каждую упаковку в наборе потребления. Если потребитель строго предпочитает x, y или безразличен между ними, то u(x) ^>₌ u(y).

Например, предположим, что потребитель, потребление набор X = {ничего, 1 яблоко,1 апельсин, 1 яблоко и 1 апельсин, 2 яблока, 2 апельсина}, и его служебная функция u(ничего) = 0, u(1 яблоко) = 1, u(1 флакон) = 2, u(1 яблоко и 1 апельсин) = 5, u(2 яблокa) = 2 и u(2 апельсинов) = 4. Тогда этот потребитель предпочитает 1 апельсин 1 яблоку, но предпочитает по одному из каждого из них 2 апельсинам.

В микроэкономических моделях (Microeconomics) обычно существует конечный набор из L товаров, и потребитель может потреблять произвольное количество каждого товара. Это дает набор потребления R₊^L и каждая упаковка x {- R₊^L представляет собой вектор, содержащий суммы каждого товара. В предыдущем примере мы могли бы сказать, что есть два товара: яблоки и апельсины. Если мы говорим, что яблоки - это первый товар, и апельсины второй, то формула будет X=R₊² и у набора (0, 0)=0, у (1, 0)=1, у (0, 1)=2, у (1, 1)=4, у (2, 0)=2, у (0, 2)=3, как раньше. Обратите внимание, что для u, чтобы быть полезной функцией на X, он должен быть определен для каждого пакета в X? поэтому теперь функция должна быть определена и для дробных яблок и апельсинов. Одна функция, которая соответствовала бы этим числам, - это u(x_яблоки,x_{апельсины}) = x_яблоки+2x_{апельсины}+2x_яблокиx_{апельсины}.

Функция полезности u:X -> R представляет отношение предпочтения _^< на X iff (если и только если) для каждого x,y {- X. u(x) _{_}^< u(y) подразумевает x _^< y. Если u представляет _^<, то это означает, что он является полным и транзитивным, а следовательно, рациональным.

Во многих моделях принятия решений функции полезности определяются формулировкой задачи. В некоторых ситуациях предпочтение лица, принимающего решение, должно быть вызвано и представлено скалярной функцией полезности (или цели). Существующие методы построения таких функций собраны в трудах двух специализированных конференций. Математические основы наиболее распространенных типов функций полезности — квадратичных и аддитивных — были заложены Жераром Дебре[6][7] а методы их построения как из порядковых, так и из кардинальных данных, в частности из интервью с лицом, принимающим решение, были разработаны Андраником Тангианом.[8][9]

В финансовых приложениях, например, при оптимизации портфеля, инвестор выбирает финансовый портфель, который максимизирует его/ее собственную функцию полезности или, что эквивалентно, минимизирует его/ее меру риска. Например, современная портфельная теория выбирает дисперсию в качестве меры риска; другими популярными теориями являются теория ожидаемой полезности [3] и теория перспектив, [4] чтобы определить конкретную функцию полезности для любого данного инвестора, можно построить процедуру анкетирования с вопросами в виде: сколько вы заплатите за X% шанс получить y? Теория выявленных предпочтений предлагает более прямой подход: рассмотрим портфель X*, который в настоящее время принадлежит инвестору, а затем найти функцию полезности/меру риска, такую что X* становится оптимальным портфелем.[5]

Для упрощения расчетов были сделаны различные альтернативные предположения относительно деталей человеческих предпочтений, и они подразумевают различные альтернативные функции полезности, такие как:

• CES (constant elasticity of substitution, or isoelastic) utility (Полезность CES - постоянная эластичность замещения, или изоэластичность)
• Isoelastic utility (Изоэластичная полезность)
• Exponential utility (Экспоненциальная полезность)
• Quasilinear utility (Квазилинейная полезность)
• Homothetic preferences (Гомотетические предпочтения)
• Stone–Geary utility function (Функция полезности Stone–Geary)
• Gorman polar form (Полярная форма Гормана)

• Greenwood–Hercowitz–Huffman preferences (Предпочтения Greenwood-Hercowitz-Huffman)
• King–Plosser–Rebelo preferences (Кинг-Плоссер-Ребело предпочтения)

• Hyperbolic absolute risk aversion (Гиперболическое абсолютное неприятие риска)

Большинство функций полезности, используемых в моделировании или теории, хорошо себя ведут. Они обычно монотонны и квазивогнуты. Однако предпочтения могут быть не представлены функцией полезности. Примером могут служить лексикографические предпочтения, которые не являются непрерывными и не могут быть представлены непрерывной функцией полезности.[6]

Основная статья: гипотеза ожидаемой полезности

Теория ожидаемой полезности имеет дело с анализом выбора между рискованными проектами с множественными (возможно, многомерными) результатами.

Петербургский парадокс был впервые предложен Николаем Бернулли в 1713 году и разрешен Даниэлем Бернулли в 1738 году. Д. Бернулли утверждал, что парадокс может быть разрешен, если лица, принимающие решения, проявляют отвращение к риску, и доказывал логарифмическую кардинальную функцию полезности. (Анализ данных международных обследований в XXI веке показал, что в той мере, в какой полезность представляет собой счастье, как и в утилитаризме, она действительно пропорциональна логарифмическому доходу.)

Первое важное использование теории ожидаемой полезности было сделано Джоном фон Нейманом и Оскаром Моргенштерном, которые использовали предположение о максимизации ожидаемой полезности в своей формулировке теории игр.

Основная статья: теорема полезности фон Неймана–Моргенштерна

Фон Нейман и Моргенштерн рассматривали ситуации, в которых результаты выбора не известны с уверенностью, но имеют вероятности, связанные с ними.

Обозначение для лотереи выглядит следующим образом: если варианты A и B имеют вероятность p и 1-p в лотерее, мы пишем его как линейную комбинацию:

В более общем плане, для лотереи с большим количеством возможных вариантов:

Сделав некоторые разумные предположения о том, как ведут себя выборы, фон Нейман и Моргенштерн показали, что если агент может выбирать между лотереями, то этот агент имеет функцию полезности, такую что желательность произвольной лотереи может быть вычислена как линейная комбинация полезностей ее частей, с весами, являющимися их вероятностями возникновения.

Это называется теоремой об ожидаемой полезности. Необходимые допущения - это четыре аксиомы о свойствах отношения предпочтения агента перед "простыми лотереями", которые являются лотереями всего с двумя вариантами. Написание B_{_}^<A означает, что "A слабо предпочтительнее B" ("A предпочтительнее, по крайней мере, столько же, сколько и B"), аксиомы являются:

1. полнота: для любых двух простых лотерей L и M, либо L[sup]<[/sup]_M или M[sup]<[/sup]_L, либо одинаковы и в этом случае они рассматриваются как одинаково желательные).
2. транзитивность: для любых трех лотерей L, M, N если L[sup]<[/sup]_M[sup]<[/sup]_N, то L[sup]<[/sup]_N.
3. выпуклость/непрерывность (свойство Архимеда): если L[sup]<[/sup]_M[sup]<[/sup]_N, то существует p между 0 и 1 такой, что лотерея pL+(1-p)N одинаково желательна как и M.
4. независимость: для любых трех лотерей L,M,N и любой вероятности p, L[sup]<[/sup]_M если и только если pL+(1-p)N[sup]<[/sup]_ pM+(1-p)N. Интуитивно понятно, что если лотерея образована вероятностной комбинацией L и N является не более предпочтительной, чем лотерея, образованная той же вероятностной комбинацией M и N, тогда, и только тогда L[sup]<[/sup]_ M.

Аксиомы 3 и 4 позволяют нам решить об относительной полезности двух активов или лотерей.

На более формальном языке: функция полезности фон Неймана-Моргенштерна-это функция от выбора до (натуральных) действительных чисел:

который присваивает реальное число (номер) каждому результату таким образом, что захватывает предпочтения агента по сравнению с простыми лотереями. Согласно четырем упомянутым выше предположениям, агент предпочтет лотерею L₂ лотерее L₁ тогда и только тогда, когда для функции полезности, характеризующей этого агента, ожидаемая полезность L₂ больше, чем ожидаемая полезность L₁:

Из всех аксиом наиболее часто отбрасывается независимость. Возникло множество обобщенных теорий ожидаемой полезности, большинство из которых отбрасывают или ослабляют аксиому независимости.

Кастаньоли и Ликальци (1996) и Бордли и Ликальци (2000) предоставили другую интерпретацию теории фон Неймана и Моргенштерна. В частности, для любой функции полезности существует гипотетическая эталонная лотерея с ожидаемой полезностью произвольной лотереи, вероятность выполнения которой не хуже, чем у эталонной лотереи. Предположим, что успех определяется как получение результата не хуже, чем результат эталонной лотереи. Тогда эта математическая эквивалентность означает, что максимизация ожидаемой полезности эквивалентна максимизации вероятности успеха. Во многих контекстах это облегчает обоснование и применение концепции полезности. Например, полезность фирмы может быть вероятностью удовлетворения неопределенных будущих ожиданий клиентов.[7][8][9][10]

Основная статья: косвенная полезность

Косвенная функция полезности дает оптимальное достижимое значение данной функции полезности, которое зависит от цен на товары и уровня дохода или богатства, которым обладает индивид.

Одним из видов использования понятия косвенной полезности является понятие полезности денег. (Косвенная) функция полезности для денег - это нелинейная функция, которая ограничена и асимметрична относительно начала координат. Функция полезности является вогнутой в положительной области, что отражает явление уменьшения предельной полезности. Ограниченность отражает тот факт, что после определенного момента деньги вообще перестают быть полезными, так как размер любой экономики в любой момент времени сам по себе ограничен. Асимметрия относительно происхождения отражает тот факт, что получение и потеря денег могут иметь радикально различные последствия, как для отдельных лиц, так и для бизнеса. Нелинейность функции полезности для денег имеет глубокие последствия в процессах принятия решений: в ситуациях, когда результаты выбора влияют на полезность через прибыли или потери денег, которые являются нормой в большинстве бизнес-условий, оптимальный выбор для данного решения зависит от возможных результатов всех других решений в тот же период времени.[11]

Кембриджский экономист Джоан Робинсон лихо критиковала полезность за то, что она является круговой концепцией: "полезность - это качество в товарах, которое заставляет людей покупать их, и тот факт, что люди хотят покупать товары, показывает, что они имеют полезность" [12]: 48 Робинсон также указал, что поскольку теория полезности предполагает, что предпочтения фиксированы, это означает, что полезность не является проверяемым предположением. Это происходит потому, что если мы возьмем изменения в поведении людей в связи с изменением цен или изменением базового бюджетного ограничения, мы никогда не сможем быть уверены, в какой степени изменение в поведении было вызвано изменением цены или бюджетного ограничения, а в какой-изменением предпочтений.[13] Эта критика теории полезности аналогична критике философа Ганса Альберта, который утверждал, что условия ceteris paribus (при всех равных условиях), на которых покоилась маржиналистская теория спроса, делали саму теорию пустой тавтологией и полностью закрытой для экспериментальной проверки.[14] в сущности, кривая спроса и предложения (теоретическая линия количества продукта, который был бы предложен или запрошен по заданной цене) является чисто онтологической и никогда не может быть продемонстрирована эмпирически.

Другая критика концепции полезности исходит из утверждения, что ни кардиналистская полезность, ни порядковая ординалистская полезность не могут быть эмпирически наблюдаемы в реальном мире. В случае кардиналистской полезности невозможно измерить уровень удовлетворенности "количественно", когда кто-то потребляет или покупает яблоко. В случае порядковой полезности невозможно определить, какой выбор был сделан, когда кто-то покупает, например, апельсин. Любой акт будет включать предпочтение перед обширным набором вариантов (таких как яблоко, апельсиновый сок, другие овощи, таблетки витамина С, физические упражнения, а не покупки и т. д.).[15][16]

На другие вопросы о том, какие аргументы должны входить в функцию полезности, ответить трудно, но они кажутся необходимыми для понимания полезности. Независимо от того, получают ли люди пользу от согласованности желаний, убеждений или чувства долга, это ключ к пониманию их поведения в органоне полезности.[17] точно так же выбор между альтернативами сам по себе является процессом определения того, что считать альтернативами, вопросом выбора в условиях неопределенности.[18]

С точки зрения эволюционной психологии, полезность лучше рассматривать как результат предпочтений, которые максимизировали эволюционную приспособленность в наследственной среде, но не обязательно в текущей.[19]

См. также

• Law of demand (Закон спроса)
• Marginal utility (Предельная полезность)
• Utility maximization problem (Проблема максимизации полезности)
• Decision-making software